| Upomoć, spašavajte! Za sve one koji su zaglavili na nekom detalju |

|
|
 04.10.2005., 17:09
04.10.2005., 17:09
|
#1
|
|
ma dosada jel...
Registracija: Jan 2004.
Lokacija: in a galaxy far far away
Postova: 987
|
Matematika - pomoć II
jel zna netko mozda kako da napravim graf tako da mi na y nanosi jednu funkciju (npr. y(a)=2a ) a na x-os nanosi drugu funkciju (npr. x(a)=a/4)
ovo je npr. da mi nanosi samo na y-os kao funkciju $a$, za $a$ od 0 do 8
Plot[2a, {a, 0, 8}];
a ja bi sad da mi na x ne nanosi samo $a$ nego neku funkciju ( npr. x(a)=a/4 )
ajde pomozite, guglam ali mi nekako neide .. 
edit: otkrio sam help  ali ni no bas ne pomaze nesto
__________________
I'm being hunted by paleface in blue
and these cracka' spooks are haunting you too ;)
|

|

|
 04.10.2005., 19:56
04.10.2005., 19:56
|
#2
|
|
Ponekad nisam na forumu
Registracija: Dec 2002.
Postova: 9,354
|
Re: mathematica
Quote:
grimReaper kaže:
jel zna netko mozda kako da napravim graf tako da mi na y nanosi jednu funkciju (npr. y(a)=2a ) a na x-os nanosi drugu funkciju (npr. x(a)=a/4)
ovo je npr. da mi nanosi samo na y-os kao funkciju $a$, za $a$ od 0 do 8
Plot[2a, {a, 0, 8}];
a ja bi sad da mi na x ne nanosi samo $a$ nego neku funkciju ( npr. x(a)=a/4 )
ajde pomozite, guglam ali mi nekako neide .. 
edit: otkrio sam help  ali ni no bas ne pomaze nesto ali ni no bas ne pomaze nesto
|
Davno je to bilo kada sam se s ovim problemom natezao. Uglavnom, rjesio sam ga tako da se jedan graf 'nalijepi' na drugi. Mislim da se pri tome koristi naredba PlotTogether pa dalje sto se zeli.
No, mozes problem i elegantnije rijesiti. Ako ti je ova druga funkcija na x-osi dobro definirana za cijelo podrucje, tada napravi inverz funkcije, i nju normalno nacrtaj. Dakle, za gornji slucaj nacrtas funkciju y(x)=4x
__________________
The only way of finding the limits of the possible is by going beyond them into the impossible. (A. Clarke)
Obnovljeni astronomski blog
|

|

|
 04.10.2005., 21:27
04.10.2005., 21:27
|
#3
|
|
ma dosada jel...
Registracija: Jan 2004.
Lokacija: in a galaxy far far away
Postova: 987
|
Re: Re: mathematica
Quote:
El Tomo kaže:
Davno je to bilo kada sam se s ovim problemom natezao. Uglavnom, rjesio sam ga tako da se jedan graf 'nalijepi' na drugi. Mislim da se pri tome koristi naredba PlotTogether pa dalje sto se zeli.
No, mozes problem i elegantnije rijesiti. Ako ti je ova druga funkcija na x-osi dobro definirana za cijelo podrucje, tada napravi inverz funkcije, i nju normalno nacrtaj. Dakle, za gornji slucaj nacrtas funkciju y(x)=4x
|
moze malo ovaj prvi nacin u detalje sta i kako da napisem, ako se sjecas, u helpu mi nista ne izbacuje za PlotTogether, a meni je to jako novo
a sto se tice drugog nacina, obje funkcije su sinusoide 
__________________
I'm being hunted by paleface in blue
and these cracka' spooks are haunting you too ;)
|

|

|
 09.10.2013., 18:59
09.10.2013., 18:59
|
#4
|
|
Registrirani korisnik
Registracija: Oct 2013.
Postova: 1
|
poooooomoć
1 + 1 + 1
x + y +z = - - - = 1 (1 kroz x + 1 kroz ypsilon + 1 kroz z )
x y z
x3 + y3 + z3 = 1 (ovo je sve x, y, z na treću)
U P O M O Ć !
|

|

|
 09.10.2013., 22:45
09.10.2013., 22:45
|
#5
|
|
x² π ℯ ∞ α β
Registracija: May 2008.
Postova: 144
|
Quote:
matematikagym kaže:

1 + 1 + 1
x + y +z = - - - = 1 (1 kroz x + 1 kroz ypsilon + 1 kroz z )
x y z
x3 + y3 + z3 = 1 (ovo je sve x, y, z na treću)
|
1/x + 1/y + 1/z = 1
x^3 + y^3 + z^3 = 1
je li to tako?
__________________
I tako to!
|

|

|
 04.10.2005., 21:48
04.10.2005., 21:48
|
#6
|
|
ma dosada jel...
Registracija: Jan 2004.
Lokacija: in a galaxy far far away
Postova: 987
|
tek sam sad skuzio .. pa ovo je glupo (?) mislim sta dobit cu na x izmedju -4 i 4 a na y izmedju -8 i 8 , i cini mi se da uopce nece ispast graf nego jedna velika fleka 
__________________
I'm being hunted by paleface in blue
and these cracka' spooks are haunting you too ;)
|

|

|
 10.07.2012., 21:49
10.07.2012., 21:49
|
#7
|
|
Registrirani korisnik
Registracija: Jul 2011.
Postova: 1
|
pomoć
jel zna itko kako se riješava linearna aproksimacija i tangencijala ravnina u Mathematici? izračunala sam derivacije sad samo ne mogu to složit u formulu da mi izračuna
|

|

|
 12.07.2012., 03:46
12.07.2012., 03:46
|
#8
|
|
Registrirani korisnik
Registracija: Feb 2008.
Postova: 275
|
Quote:
tinapk kaže:

jel zna itko kako se riješava linearna aproksimacija i tangencijala ravnina u Mathematici? izračunala sam derivacije sad samo ne mogu to složit u formulu da mi izračuna
|
Ako znaš što je linearna aproksimacija i tangencijalna ravnina, onda ti pomoć i ne treba jer je to praktički uvrštavanje formula u Mathematici. Ako ne znaš, onda se prvo pozabavi sa tim pojmovima i ako ti svejedno neće ići onda se javi ali i napiši što si sve napravila do sad. ( ne opisno nego copy paste ovdje taj .nb file u kojem imaš rješenje ) |

|

|
 12.07.2012., 04:56
12.07.2012., 04:56
|
#9
|
|
Registrirani korisnik
Registracija: Apr 2008.
Postova: 85
|
Riješite integral:
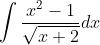
Zadatak sam pokušao riješiti uz pomoć WolframAlphe, ali mi nikako ne ide.
Probam sa supstitucijom u=sqrt(x+2), du=1/(2sqrt(x+2))dx, dx=2sqrt(x+2)du, krenem nešto kombinirat, ali se onda u cijelom tom procesu zapetljam jer što god dalje idem sve postaje mnogo kompliciranije.
Zapeo sam i trebam pomoć. |

|

|
 12.07.2012., 13:57
12.07.2012., 13:57
|
#10
|
|
Registrirani korisnik
Registracija: Feb 2011.
Lokacija: Rijeka
Postova: 360
|
Quote:
Tartaros kaže:

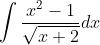
Zadatak sam pokušao riješiti uz pomoć WolframAlphe, ali mi nikako ne ide.
Probam sa supstitucijom u=sqrt(x+2), du=1/(2sqrt(x+2))dx, dx=2sqrt(x+2)du, krenem nešto kombinirat, ali se onda u cijelom tom procesu zapetljam jer što god dalje idem sve postaje mnogo kompliciranije.
Zapeo sam i trebam pomoć. |
Ne kažem da se ne može supstitucijom ali vjerujem ti na riječ da se jako zakomplicira. Ovako sam to ja riješio, nadopunjavanjem do nazivnika.

Dakle imaš na kraju tri integrala za riješiti, ja sam to sve vukao u jednoj kobasici jer mi je bilo najjednostanije za c/p ali prati jedan po jedan razlomak što se s njim događa i bit će ti jasnije.
1) Nadopuna do kvadrata binoma nazivnika (stavio sam u zagradu da bude jasnije) -> (x+2)^2
2)"Višak" prebaci u drugi intergral, nadopuna do nazivnika x+2
3) Ponovno višak prebaci u treći integral koji je najobičniji n*(1/nazivnik)
Pitaj što nije jasno. |

|

|
 12.07.2012., 18:41
12.07.2012., 18:41
|
#11
|
|
Registrirani korisnik
Registracija: Feb 2008.
Postova: 275
|
Quote:
Tartaros kaže:

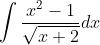
Zadatak sam pokušao riješiti uz pomoć WolframAlphe, ali mi nikako ne ide.
Probam sa supstitucijom u=sqrt(x+2), du=1/(2sqrt(x+2))dx, dx=2sqrt(x+2)du, krenem nešto kombinirat, ali se onda u cijelom tom procesu zapetljam jer što god dalje idem sve postaje mnogo kompliciranije.
Zapeo sam i trebam pomoć. |
Pa ne postaje kompliciranije nego dosta jednostavnije, pretpostavljam da si negdje fulao u procesu.
\cdot (x+1)}{\sqrt{x+2}}}dx = \int{\frac{((x+2)-3)\cdot ((x+2)-1)}{\sqrt{x+2}}}dx = \\ = \{\begin{array}{c} u = \sqrt{x+2}\\ 2du=\frac{dx}{\sqrt{x+2}} \end{array}\} = \int{(u^2-3)(u^2-1)2du} = 2\int{(u^4-4u^2+3)du})
Što je dalje dosta lagano rješiti, s tim da samo nakon rješavanj integrala vratiš supstituciju. |

|

|
 12.07.2012., 19:05
12.07.2012., 19:05
|
#12
|
|
Registrirani korisnik
Registracija: Jun 2009.
Lokacija: Zagreb
Postova: 89
|
U velikoj mjeri slično, ako te zbunjuje rastavljanje u brojniku, je i ovo rješenje:
^2-1}{\sqrt{t^2}}\,%202t\,%20dt=\\[12pt]%202\int\frac{t^4-4t^2+4-1}{t}\,%20t\,%20dt%20=%202\int(t^4-4t^2+3)\,%20dt) |

|

|
 12.07.2012., 21:08
12.07.2012., 21:08
|
#13
|
|
Registrirani korisnik
Registracija: Apr 2008.
Postova: 85
|
Quote:
Crori_ kaže:

Ne kažem da se ne može supstitucijom ali vjerujem ti na riječ da se jako zakomplicira. Ovako sam to ja riješio, nadopunjavanjem do nazivnika.
http://img339.imageshack.us/img339/6...25ba54d3a0.png
Dakle imaš na kraju tri integrala za riješiti, ja sam to sve vukao u jednoj kobasici jer mi je bilo najjednostanije za c/p ali prati jedan po jedan razlomak što se s njim događa i bit će ti jasnije.
1) Nadopuna do kvadrata binoma nazivnika (stavio sam u zagradu da bude jasnije) -> (x+2)^2
2)"Višak" prebaci u drugi intergral, nadopuna do nazivnika x+2
3) Ponovno višak prebaci u treći integral koji je najobičniji n*(1/nazivnik)
Pitaj što nije jasno. |
Razumijem sve što si napisao, hvala za ovako detaljan postupak. Inače, riješit se razlomka na ovakav nekakav način mi i jest bio prvi plan, ali sam onda htio vidjet šta Wolfram kaže, pa sam probao sa supstitucijom.
Quote:
Cobs kaže:

Pa ne postaje kompliciranije nego dosta jednostavnije, pretpostavljam da si negdje fulao u procesu.
\cdot (x+1)}{\sqrt{x+2}}}dx = \int{\frac{((x+2)-3)\cdot ((x+2)-1)}{\sqrt{x+2}}}dx = \\ = \{\begin{array}{c} u = \sqrt{x+2}\\ 2du=\frac{dx}{\sqrt{x+2}} \end{array}\} = \int{(u^2-3)(u^2-1)2du} = 2\int{(u^4-4u^2+3)du})
Što je dalje dosta lagano rješiti, s tim da samo nakon rješavanj integrala vratiš supstituciju. |
U pravu si, fulam u procesu, i poslije toga sve se raspada. Da budem iskren, integral i razlomak su me malo zastrašili i zbunili.
Postoji li neki univerzalni način pristupa kad je integriranje razlomka u pitanju? Kako najbolje ocijeniti najlakši način za rješavanje problema?
Quote:
Matematko kaže:

U velikoj mjeri slično, ako te zbunjuje rastavljanje u brojniku, je i ovo rješenje:
^2-1}{\sqrt{t^2}}\,%202t\,%20dt=\\[12pt]%202\int\frac{t^4-4t^2+4-1}{t}\,%20t\,%20dt%20=%202\int(t^4-4t^2+3)\,%20dt) |
Ovo mi se zapravo čini kao najintuitivniji pristup, šteta što se ja nisam toga sjetio.
Uglavnom, hvala vam ljudi, od velike je pomoći kad vidiš kako jedan problem riješiti na tri različita načina. |

|

|
 26.07.2012., 09:00
26.07.2012., 09:00
|
#14
|
|
Registrirani korisnik
Registracija: Jul 2012.
Postova: 21
|
Postotci
Može li pomoć oko ovih zadataka?
1.) Osobe C i D dijele iznos od 36 100 kn, Koliko će dobiti osoba D ako osoba C dobiva 10% manje od osobe D?
2.) Plin je poskupio 15% . Koliko treba pojeftiniti da bi mu krajnja cijena 5.5% veća od cijene prije poskupljenja?
Hvala unaprijed!
|

|

|
 26.07.2012., 16:44
26.07.2012., 16:44
|
#15
|
|
Registrirani korisnik
Registracija: Apr 2011.
Lokacija: Land Down Under
Postova: 953
|
1)Dvije osobe dijele 36100 kn na pola prvo-18050 kn. Jedna osoba će dobiti 10% više od druge-1805kn.
Osoba D-19855 kn
Osoba C-16245 kn
2) Uzmeš da je cijena plina sada 100 kn. Nakon poskupljenja cijena je 115.
cijena koju tražiš je 5.5% veća od početne- 105.5.
I sad se pitaš koliko treba pojeftiniji ovaj plin od 115kn da bi cijena bila 105,5 kn.
115-105,5=9,5
9,5/115=8,26%
Dali netko zna objasniti što bi bio totalni diferencijal funkcije i zasto se on koristi? Isto tako i gradijent funkcije?
Bilo bi lijepo ako bi netko to znao malo životnije, slikovitije objasnit pogotovo totalni diferencijal.
Hvala  |

|

|
 28.07.2012., 23:17
28.07.2012., 23:17
|
#16
|
|
Registrirani korisnik
Registracija: Jul 2011.
Postova: 63
|
ljudii, jedno jednostavno ali istovremeno i meni jako komplicirano pitanje.
sada sam na internetu našla jedan zadatak, kojiglasi ovako.
48/2*(9+3)
koliko je rjeeeeeeeeešenje?
kako ide redosljed?
jeli rješenje 288 ili 2 
hvala na pomoćiii
__________________
:)
|

|

|
 29.07.2012., 15:03
29.07.2012., 15:03
|
#17
|
|
Registrirani korisnik
Registracija: May 2010.
Postova: 45
|
Dan je sljedeći niz razlomaka:
1/1
1/2 , 2/2 , 1/2
1/3 , 2/3 , 3/3 , 2/3 , 1/3
1/4 , 2/4 , 3/4 , 4/4 , 3/4 , 2/4 , 1/4
.
.
.
Brojnik 2001. razlomka je ?
25?
Zadnje uređivanje Roberty7 : 29.07.2012. at 15:10.
|

|

|
 29.07.2012., 21:27
29.07.2012., 21:27
|
#18
|
|
Registrirani korisnik
Registracija: Feb 2008.
Postova: 275
|
Quote:
Roberty7 kaže:

Dan je sljedeći niz razlomaka:
1/1
1/2 , 2/2 , 1/2
1/3 , 2/3 , 3/3 , 2/3 , 1/3
1/4 , 2/4 , 3/4 , 4/4 , 3/4 , 2/4 , 1/4
.
.
.
Brojnik 2001. razlomka je ?
25?
|
Vidiš da je u svakom redu točno neparan broj razlomaka i to idu po redu
( 1 red - 1 )
( 2 red - 3 )
( 3 red - 5 )
( 4 red - 7 )
( itd. )
znači da ne brojimo na prste mene recimo zanima koji je razlomak po redu odmah u 5. redu? ( znam da je 1/5 ali ne znam koji je on po redu a to me zanima ). Znam da je ispred njega 1+3+5+7 razlomaka, znači on je 1+3+5+7+1 po redu. Tj. ispred njega će biti točno toliko razlomaka koliko je zbroj prvih 4 neparnih brojeva. Isto tako vrijedi i za recimo 20 red, da je ispred prvog razlomka u 20. redu točan broj razlomaka koliki je zbroj prvih 19 neparnih brojeva. Pa sljedeće što nas zanima postoji li neka općenita formula za zbroj prvih n neparnih brojeva. Da ne bi sami to zmišljali, ( makar ni to nije tak teško kak se čini ) lagano se nađe na googlu da je rješenje jednako n^2.
To se da provjeriti na prvih par brojeva, a za ostale ćemo vjerovati na riječ.
1 = 1^2 = 1 ( prvi red je u redu )
1+3 = 2^2 = 4 ( drugi red je u redu )
1+3+5 = 3^2 = 9 (treći red je u redu )
1+3+5+7 = 4^2 = 16 ( cetvrti red je u redu )
... itd ...
Znači sad praktički možemo lagano izračunati koji nam je razlomak po redu prvi u svakom od redova ( u prvom redu je prvi po redu, u drugom redu drugi( 1+1 ) po redu, u trecem redu peti( 4+1 ) po redu, u cetvrtom redu deseti( 9+1 ) po redu, u petom redu sedamnaesti( 16+1 ) po redu itd. )
korijenujmo 2001 i dobiti ćemo 44.73 što znači da je 2001 između 44^2 i 45^2, što znači da je 2001 razlomak u 45 redu, pogledajmo koliko je razlomaka prije 45. reda ( 44^2 ) i dobijemo da je 44^2 = 1936. Znači prvi razlomak u 45 redu je 1937. po redu. U svakom redu je neparan broj razlomaka ( u n-tom retku točno 2*n-1 njih gdje je središnji jednak 1, dok ostali padaju prema krajevima za 1/n ). Nije teško izračunati da je središnji razlomak ( onaj koji je jedank 1 ) u 45 po redu točno 1981. ( 1936+45 ) pa se treba još pomaknuti za 20 razlomaka "u desno" da dođemo do 2001.
Prvi od tih 20 je znači: 44/45, drugi od 20 je 43/45, dvadeseti od tih 20 je (45-20)/45 tj. 25/45, pa je brojnik u tom razlomku jednak 25, a to je i rješenje postavljenog pitanja |

|

|
 30.07.2012., 11:56
30.07.2012., 11:56
|
#19
|
|
Registrirani korisnik
Registracija: May 2010.
Postova: 45
|
Quote:
Cobs kaže:

Vidiš da je u svakom redu točno neparan broj razlomaka i to idu po redu
( 1 red - 1 )
( 2 red - 3 )
( 3 red - 5 )
( 4 red - 7 )
( itd. )
znači da ne brojimo na prste mene recimo zanima koji je razlomak po redu odmah u 5. redu? ( znam da je 1/5 ali ne znam koji je on po redu a to me zanima ). Znam da je ispred njega 1+3+5+7 razlomaka, znači on je 1+3+5+7+1 po redu. Tj. ispred njega će biti točno toliko razlomaka koliko je zbroj prvih 4 neparnih brojeva. Isto tako vrijedi i za recimo 20 red, da je ispred prvog razlomka u 20. redu točan broj razlomaka koliki je zbroj prvih 19 neparnih brojeva. Pa sljedeće što nas zanima postoji li neka općenita formula za zbroj prvih n neparnih brojeva. Da ne bi sami to zmišljali, ( makar ni to nije tak teško kak se čini ) lagano se nađe na googlu da je rješenje jednako n^2.
To se da provjeriti na prvih par brojeva, a za ostale ćemo vjerovati na riječ.
1 = 1^2 = 1 ( prvi red je u redu )
1+3 = 2^2 = 4 ( drugi red je u redu )
1+3+5 = 3^2 = 9 (treći red je u redu )
1+3+5+7 = 4^2 = 16 ( cetvrti red je u redu )
... itd ...
Znači sad praktički možemo lagano izračunati koji nam je razlomak po redu prvi u svakom od redova ( u prvom redu je prvi po redu, u drugom redu drugi( 1+1 ) po redu, u trecem redu peti( 4+1 ) po redu, u cetvrtom redu deseti( 9+1 ) po redu, u petom redu sedamnaesti( 16+1 ) po redu itd. )
korijenujmo 2001 i dobiti ćemo 44.73 što znači da je 2001 između 44^2 i 45^2, što znači da je 2001 razlomak u 45 redu, pogledajmo koliko je razlomaka prije 45. reda ( 44^2 ) i dobijemo da je 44^2 = 1936. Znači prvi razlomak u 45 redu je 1937. po redu. U svakom redu je neparan broj razlomaka ( u n-tom retku točno 2*n-1 njih gdje je središnji jednak 1, dok ostali padaju prema krajevima za 1/n ). Nije teško izračunati da je središnji razlomak ( onaj koji je jedank 1 ) u 45 po redu točno 1981. ( 1936+45 ) pa se treba još pomaknuti za 20 razlomaka "u desno" da dođemo do 2001.
Prvi od tih 20 je znači: 44/45, drugi od 20 je 43/45, dvadeseti od tih 20 je (45-20)/45 tj. 25/45, pa je brojnik u tom razlomku jednak 25, a to je i rješenje postavljenog pitanja
|
Hvala,ja sam malo drukčije rješio a nisam uspio naći rješenje na internetu. Hvala još jednom  |

|

|
 30.07.2012., 18:47
30.07.2012., 18:47
|
#20
|
|
Registrirani korisnik
Registracija: Feb 2009.
Postova: 181
|
financijska matematika
Pozdrav ljudi, evo imam jedno pitanje u vezi ovog zadatka, muči me stavka a)
Vidi se na slici rješenje stavke a) pa mi nije baš jasno kako do ovih 20 000^4.
Obično takve zadatke rješavam kad su u pitanju mjesečne kamatne stope pa mi je nekako logičnije, znam da je ovdje bitna razlika jer se ukamaćuje godišnje ali kad si nacrtam tijek novca ja bih to stavila ovako
X= [9/10 * (20 000 * 1.075^3 + 10 000) * 1.075^2] * 1.065
pa mi X ispada 38 597, 67981
I imam još jedno pitanje, kako je najsigurnije izračunati ovo kad se traži umanjena stopa za nekoliko posto?
 Uploaded with ImageShack.us
Hvala |

|

|
 |
|
| Tematski alati |
|
|
| Opcije prikaza |
 Hibridni mod Hibridni mod
|
Sva vremena su GMT +2. Trenutno vrijeme je: 10:59.
|
|
|
|

